Розділи

• Загальне
  
  

  Загальне

  • 
    

    Дериглазов Л.В., Кухаренко В.М., Перхун Л.П., Товмаченко Н.М.

    Національна академія статистики,обліку та аудиту
    Національний технічний університет «Харківський політехнічний інститут»

    Статистичні методи аналізу результатів тестового контролю знань

    Постановка проблеми.

    Найважливішим питанням реформування вищої освіти в Україні є питання входження в Європейський освітній простір. Особлива увага в сучасній Європі приділяється програмі навчання протягом життя - Lifelong Learning Programme, що є наступницею програми ICT / Open & Distance Learning [1,2]. Серед найсучасніших освітніх технологій, що активно заявили про себе наприкінці ХХ століття і набули сьогодні помітного поширення в розвинутих країнах світу, є дистанційні технології навчання, які підтримують і забезпечують дистанційну освіту (ДО) [3]. Розвиток та вдосконалення форм і методів контролю навчальних досягнень, які реалізують зворотній зв’язок у навчанні повинні забезпечити підвищення якості підготовки фахівців [4]. Відповідно до постанови Кабінету Міністрів України (від 14 грудня 2011 р. № 1283) «Про затвердження порядку проведення моніторингу якості освіти» визначено механізм організації і проведення моніторингу якості освіти. Зокрема, описано етапи проведення моніторингу, одним з яких є аналіз його результатів і підготовка статистичних й аналітичних відомостей і звітів. Приєднання України до Болонського освітнього процесу стимулює модернізацію сучасного розвитку системи освіти України пов’язану упровадженням інноваційних технологій у навчальний процес, запровадженням тестування за допомогою комп’ютерного алгоритмічно-програмного забезпечення.

    Виклад основного матеріалу.

    Опрацюванню результатів тестування і моніторингових досліджень, особливостям застосування комп’ютерних технологій та  статистичній  концепції тестування значну увагу приділено в працях [8,9,10,11]. Оцінювання якості тесту вбудованої системи аналізу тестових завдань Learning Content Management System  (LCMS) MOODLE  детально описано в роботі [6,7]. Наразі система LCMS Moodle інтегрована в інформаційно-навчальне середовище НАСОА (dl.nasoa.edu.ua/moodle), зокрема повністю синхронізовані бази викладачів та студентів, кожен з яких має особистий профіль на сайті, що надає їм доступ до наукових, навчальних, методичних, нормативних та інших інформаційних ресурсів академії [4,5]. Засобами LCMS MOODLE  проводиться аналіз оцінювання якості тесту та  тестових завдань дистанційних курсів (ДК), зокрема, на рис.1, 2 наведено аналіз результатів тестового контролю знань з ДК “Економетрика”.

    Однак  для ефективного впровадження тестових методик і використання у навчальному процесі показників лише попередньої статистичної обробки не достатньо,  принцип роботи автоматизованої системи повинен ґрунтуватися на критеріях математико-статистичних методів аналізу, які дають  можливість перевіряти тестові завдання на наявність прихованих дефектів, які неможливо виявити із застосуванням експертних методів.

    
    

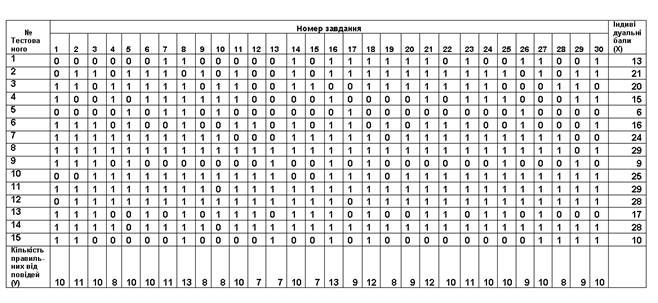
     Рис. 1. Матриця результатів тестування підсумкового тесту ДК “Економетрика

    Курс: Економетрика (Д) Grading column: Підсумковий тест Grade category current grade letters (%) current grade letters (absolute) А 29,41 5 B 11,76 2 C 11,76 2 D 11,76 2 E 0,00 0 FX 17,65 3 F 17,65 3 Sum 99,99 17

    Рис. 2.  Статистика LCMS Moodle підсумкового тесту ДК “Економетрика “.

    Визначення статистичних характеристик є головним засобом діагностики тестових властивостей завдання. Можливості застосування більш широкого спектру методів багатомірного  математико-статистичного  аналізу, зокрема  моделей дисперсійного, факторного, кластерного, дискримінантного аналізу, регресійного аналізу часових рядів,  базуються  на  використанні інструментарію професіонального програмного забезпечення пакетів статистичних програм, таких як наприклад SPSS, Statistica,  Eviews та інші.

    Об’єктивний контроль знань, вмінь і навичок вдається виконати при критеріально-орієнтованій інтерпретації тестування, яке  призначене не тільки для оцінювання рівня знань, а й для визначення рівня індивідуальних досягнень виконання тестових завдань. Тест повинен бути індивідуалізований та побудований оптимально. Успіх учасника тестування при розв’язанні деякого тестового завдання залежить від двох факторів: складності завдання і рівня підготовки учасника.

    Процес підготовки тестів, описаний в багатьох літературних джерелах [9,10]  передбачає, що складання тесту повинно проходити ряд етапів:

    1.    визначення цілей тестування,

    2.    визначення ресурсних можливостей розробників,

    3.    відбір змісту навчального матеріалу, конструювання технологічної матриці і її експертиза,

    4.    складання тестових завдань та їх експертиза,

    5.    побудова вибірки для апробації завдань і тестів,

    6.    компонування завдань для апробації, апробація тестових завдань, визначення і розрахунок показників якості тестових завдань, відбракування завдань,

    7.    складання тесту,

    8.    апробація тесту, визначення і розрахунок показників якості тесту, складання остаточного варіанта тесту.

    Апробацію та аналіз, як тестових завдань, так і тестів, може бути вирішено за допомогою Moodle [7]. В даній системі використовуються статистичні показники, які обчислюються з використанням класичної (СТТ – Classical Test Theory) та сучасної теорії тестів (IRT – Item Response Theory). Теоретичні основи цих теорій описані у роботі [10].

    Апробація є одним з важливих компонентів будь-якої системи екзаменування, що проводиться з метою оцінки професійних компетенцій. Завдання стають тестовими лише після емпіричної перевірки міри їх складності.  Завдяки коректному використанню апробації підвищуються показники якості екзаменування (валідність, надійність, об'єктивність, обґрунтованість, ефективність та прийнятність).

    Емпірично складність завдання визначається як число правильних відповідей, отриманих за кожним j-м завданням:  Rj, j=1,…,m . Для одержання об’єктивних характеристик Rj ділять на число студентів n у кожній групі (об’єм вибірки). У результаті отримаємо нормований статистичний показник – частка правильних відповідей p_j . p_j =

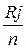
    Збільшення значення p_j означає зростання легкості завдання.

    З показником складності завдань  асоціюють  протилежну статистику – частку неправильних відповідей q_j . Вона обчислюється як відношення числа неправильних відповідей Wj (від англ. wrong – неправильний) до кількості учасників тестування n : q_j=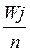, p_j+q_j=1

    Зручною мірою варіації є значення дисперсії s²_j і стандартне відхилення s_j дисперсія результатів студентів по j -ому завданню:сумарних балів учасників тестування.

    

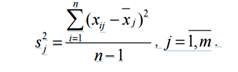
    Якщо успішність виконання j -ого завдання оцінюється балами 0 чи 1, то міра варіації визначається формулою s²_j=p_j(1-p_j) або s²_j =p_j∙q_j.

    Якщо за кожну правильну відповідь на завдання випробуваному давати 1 бал, а за неправильну відповідь або пропуск завдання - 0 балів, то профіль відповідей студента матиме вигляд послідовності з одиниць і нулів. Оскільки кожна одиниця або нуль з'являються в результаті взаємодії випробуваного до завдання, то найбільш адекватною формою подання спостережуваних результатів виконання тесту служить матриця, тобто прямокутна таблиця, що зводить воєдино профілі відповідей студентів і профілі завдань тесту (стовпці з оцінок всіх студентів з кожного завдання тесту). Приклад матриці спостережуваних результатів, отриманої при виконанні n (n = 10) студентами m (m = 10) завдань тесту при дихотомічних оцінках (1 або 0) за завданнями наведено в табл. 1 [9] , а на рис.3  відповідна гістограма, яка побудована з використанням ПСП Statistica.

    
    

    Таблиця 1.

    Матриця результатів тестування

    
    

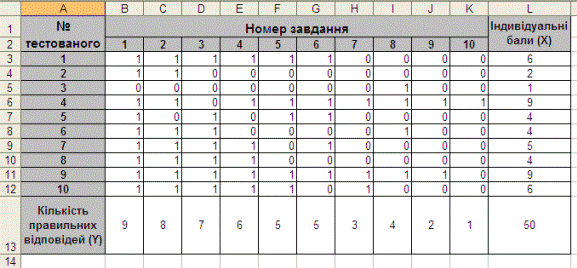
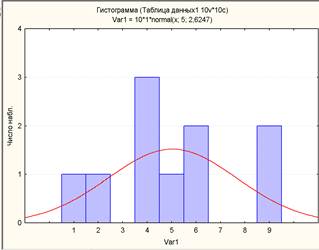
    Рис.3. Гістограма дихотомічного тесту 1.

    
    

    Для тесту х за  даними табл.1 отримаємо значення дисперсії s²_х і стандартне відхилення s_х сумарних балів учасників тестування.

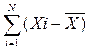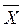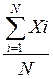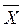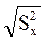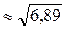
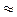    S²_x=(²)/(N-1), =, =5, S_x=, S_x2,62.

    Застосувавши формулу

    

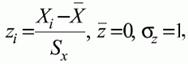
    отримаємо нормований нормальний розподіл із середнім в нулі і одиничним стандартним відхиленням.

    Якщо тест забезпечує розподіл балів, близький  до нормального, то це означає, що на його основі можна визначити стійке середнє, яке приймається в якості однієї з репрезентативних норм виконання тесту

    

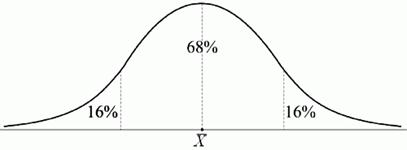
    Рис.4. Нормальна крива розподілу індивідуальних балів

     

    Для вираження ступеня відповідності між результатів виконання однієї групою (виконавців) студентів двох тестів X і Y використовується спеціальна міра, яка називається коваріацією.

    

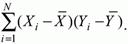
    Для підвищення порівнянності оцінок показників зв'язку за вибірками з різною дисперсією ковариацию ділять на стандартні відхилення. В результаті після перетворень виходить величина, яка називається коефіцієнтом кореляції Пірсона r_ху:

    

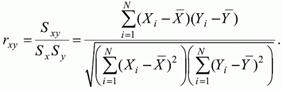
    Оскільки результати виконання завдань представляються в дихотомічної шкалою (стовпці з нулів і одиниць в матриці даних по тесту), то коефіцієнт Пірсона для дихотомічних даних обчислюється за формулою:

    

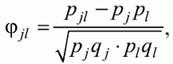
    де p_jl - частка випробовуваних, які виконали правильно обидва завдання з номерами j і l, тобто частка тих, хто отримав 1 бал за обома завданнями; p_j - частка випробовуваних, що правильно виконали j-е завдання, q_j = 1 -p_j; p_l - частка випробовуваних, що правильно виконали i-е завдання тесту, q_l = 1 - p_l.

    Наприклад, для розглянутого прикладу матриці коефіцієнт кореляції Пірсона між результатами по 5-му і 6-му завдань тесту буде:

    

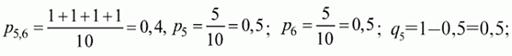
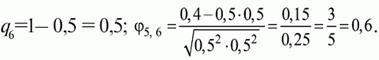
    Результати підрахунку значень коефіцієнта кореляції між усіма завданнями для прикладу матриці виконані в ПСП SPSS (змінні z₁,…,z₁₀) та зведені в табл.2.

    Далі за допомогою підрахунку значень точкового бісеріальний коефіцієнта кореляції можна оцінити валідність окремих завдань тесту. Бісеріальний коефіцієнт кореляції використовується в тому випадку, коли один набір значень розподілу задається  дихотомічної шкалою, а інший - інтервальною. Під цю ситуацію підпадає підрахунок кореляції між результатами виконання кожного завдання (дихотомічна шкала) і сумою балів випробовуваних (інтервальна або квазіінтервальная шкала) за завданнями тесту. Бісеріальний індекс дискримінації – коефіцієнт кореляції між балом за весь тест і балом за дане ТЗ, що оцінюється 1 або 0. Вказує, наскільки добре дане ТЗ розрізняє екзаменованих з високим балом і екзаменованих з низьким балом. Може змінюватися від  - 1 до + 1.  Якщо ця величина дорівнює 0, то це означає, що усі екзаменовані відповіли однаково добре або однаково погано

    Таблиця.2.   

    Коефіцієнти кореляції Пірсона між усіма завданнями

    

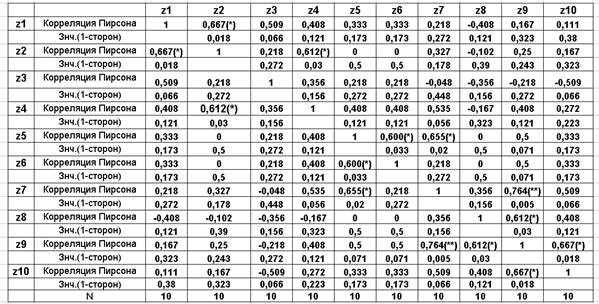
    *  Корреляция значима на уровне 0.05 (1-сторон.).

    **  Корреляция значима на уровне 0.01 (1-сторон.)

    Формула для обчислення значення точкового бісеріальний коефіцієнта r_pbis, має вигляд:

    

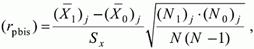
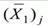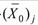    де  - середнє значення індивідуальних балів випробовуваних, які виконали вірно j-е завдання тесту; - середнє значення індивідуальних балів випробовуваних, які виконали невірно j-е завдання тесту; S_x - стандартне відхилення по безлічі значень індивідуальних балів; (N₁)_j - число випробовуваних, які виконали вірно j-е завдання тесту; (N₀)_j - число випробовуваних, які виконали невірно j-е завдання тесту; N - загальне число випробовуваних, N = N1 + N0.

    Застосування формули  для даних по 5-му завданням даного прикладу матриці дає досить високе значення точкового бісеріальний коефіцієнта.

    

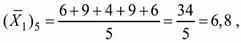
    так як 1, 4, 5, 9 і 10-й випробувані виконали завдання 5 вірно.

    

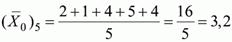
    так як 2, 3, 6, 7 і 8-й випробувані виконали завдання 5 невірно.

    Стандартне відхилення, підрахована для розглянутого прикладу раніше, Sx= 2,6; (N₁)_j = (N₀)_j =5; N = 10.

    

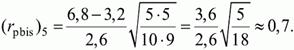
    Значення коефіцієнта бісеріальний кореляції для 10 тестових завдань отримані з використанням ПСП SPSS (рис.5) та приведені в табл. 3.

    Таблиця 3.

     Значення коефіцієнта бісеріальної кореляції для 10 тестових завдань

    Завдання	1	2	3	4	5	6	7	8	9	10
    (rpbis)j	0,535	0,502	0,263	0,738	0,723	0,643	0,789	0,246	0,803	0,535

    Для обчислення коефіцієнта бісеріальної кореляції засобами  ПСП SPSS виконуємо наступні дії.

    ^{Анализ              Описательные статистики              Таблицы сопряженности}

    

    Рис.5 Обчислення значення коефіцієнта бісеріальної кореляції

     (статистика Эта)

    Направленные меры

    			Значение
    Номинальная по интервальной	Эта	Z	0,535
    		z1

    В обчисленнях ПСП SPSS змінній Z відповідають значення первинних балів тестованих за тест, z1 – відповіді тестованих на перше завдання. (r_bis)₁=0,535.

    Для дослідження надійності тесту   використовується  двофакторний дисперсійний аналіз без повторних вимірювань, де в якості факторів використовуються тестовані та завдання, а в якості залежної змінної виступають первинні бали. В табл. 4. приведені результати значення критерія Фішера та статистичної значущості  впливу факторів для даних табл.1 з використанням ПСП SPSS (рис.6).

     

    ^{Анализ              Общая линейная модель               ОЛМ-одномерная}

    

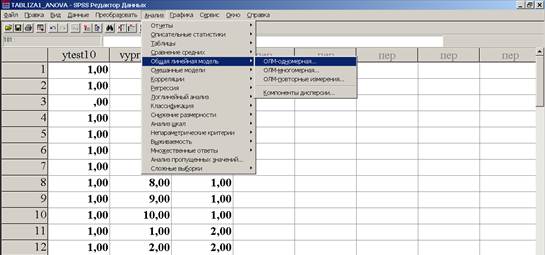
    Рис. 6.  Двофакторний дисперсійний  аналіз без повторних вимірювань засобами ПСП SPSS.

     

    Таблиця 4.

    Результати двофакторного дисперсійного аналізу даних табл.1 засобами ПСП SPSS.

                                                   Оценка эффектов межгрупповых факторов

    Зависимая переменная: ytest10

    Источник		Сумма квадратов типа III	ст.св.	Средний квадрат	F	Знач.
    vypr_t10	Гипотеза	6,200	9	,689	4,359	,000
    	Ошибка	12,800	81	,158(a)
    zawdan_t10	Гипотеза	6,000	9	,667	4,219	,000
    	Ошибка	12,800	81	,158(a)
    vypr_t10 * zawdan_t10	Гипотеза	12,800	81	,158	.	.
    	Ошибка	,000	0	.(b)

    a   MS(vypr_t10 * zawdan_t10)

    b   MS(Ошибка)

    Аналіз результатів табл.4 свідчать про статистичну значущість  впливу двох факторів: x1 – фактор тестових питань, х2 – фактор тестованих на залежну змінну у – індивідуальні  первинні бали і-ого тестованого на питання j.

    В роботі [11] для дослідження надійності тесту   пропонується так званий коефіцієнт генералізаціі, який обчислюється  з використанням результатів двофакторного дисперсійного аналізу без повторних вимірювань, де в якості факторів використовуються тестовані та завдання, а в якості залежної змінної виступають первинні бали. З використанням даних табл.1 та результатів дисперсійного аналізу табл.4 коефіцієнт генералізаціі обчислюється наступним чином.

    

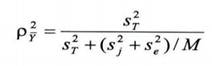
    s²_n=(MS_n-MS_r)/M=(0,689-0,158)/10=0,531,

    s²_j=(MS_j-MS_r)/N=(0,667-0,158)/10=0,509,

    s²_ε=0,158,

    ρ²_Y= s²_n/(s²_n +(s²_j+s²_ε)/M)= 0,531/(0,531+(0,509+0,158)/10)=0,8884

    Коефіцієнт генералізаціі дозволяє зі статистичних позицій оцінити надійність тестових вимірювань. Як правило, тести з надійністю менше 0,8 вважаються непридатними в професійно організованих службах і центрах тестування. Значення коефіцієнта надійності, що перевищують 0,9, говорять про високу якість тесту. Вони вкрай бажані, але не часто трапляються. Зазвичай в тестологічній практиці надійність тестів коливається в інтервалі (0,8; 0,9). Тому обчилення тесту за даними табл. 1 з ρ²_Y= 0,8884 свідчать про високу надійність цього тесту.

    Метод кластерного аналізу використовуться для кластеризації тестованих на три  кластери за якістю знань: слабкий- код кластера “2”, середній- код кластера  “1”, високий рівень- код кластера “3”.За даними табл. 1 засобами ПСП SPSS з використанням процедури ієрархічного кластерного аналізу отримані результати , які представлені дендрограмою на рис. 7, табл.5

    ^{Анализ                  классификация                              иерархическая кластеризация}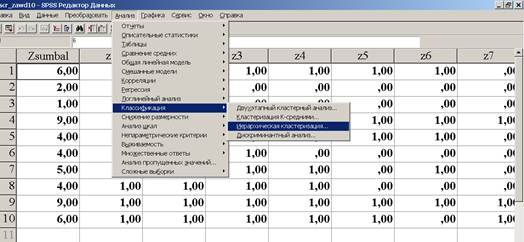

    

    Рис.7. Процедура ієрархічного кластерного аналізу в ПСП SPSS

    

    Рис.8. Дендрограма кластеризації тестованих за даними табл.1.

     

    Таблиця 5.

     Результати кластеризації тестованих за даними табл.1

    Тестовані	Первинний бал	Належність до  кластера, як результат процедури ієрархічного кластерного аналізу ПСП SPSS
    1	6,0	1
    2	2,0	2
    3	1,0	2
    4	9,0	3
    5	4,0	1
    6	4,0	2
    7	5,0	1
    8	4,0	1
    9	9,0	3
    10	6,0	1

     

    В табл.5 ідентифікатор кластера тестованих  за якістю знань позначається наступнм чином : слабкий- кластер “2”, середній- кластер “1” та високий рівень- кластер “3”.

    Результати  кластерного аналізу  для побудованих трьох  кластерів тестованих  за якістю знань використовуються для побудови параметрів моделі дискримінантного аналізу з використанням в якості  змінних трьох дискримінантних функцій  значень  відповідей тестованих на завдання технологічної матриці. Слід зауважити, що при  використанні процедури дискримінантного аналіза в ПСП SPSS відкидаються не інформативні завдання. До цих завдань відносяться легкі завдання (100%  тестованих дають правильну відповідь) та важкі завдання (100%  тестованих не дають правильну відповідь). Результати дискримінантного аналізу за даними табл. 1 наведені на рис. 9 – процедура дискримінантного аналізу в ПСП SPSS,  рис.10 -територіальна карта результатів ПСП SPSS дискримінантного аналізу та табл.6 – параметри лінійних дискримінантних функцій Фішера, табл.7 – резульати классификації.

     

    ^{Анализ                  классификация                              дискриминантный анализ}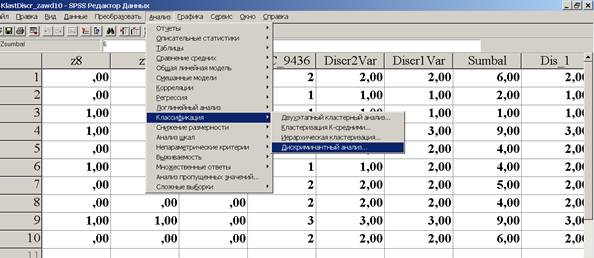

    

    Рис. 9 – процедура дискримінантного аналізу в ПСП SPSS

     

    Таблиця . 6.

    Лінійні дискримінантні функції Фішера

    Коэффициенты классифицирующей функции

    	KlasDiscr
    	1,00	2,00	3,00
    Zsumbal	28,000	84,000	161,000
    z1	35,000	105,000	175,000
    z2	-56,000	-175,000	-322,000
    z3	,000	14,000	7,000
    z4	-7,000	-14,000	-35,000
    z5	-42,000	-126,000	-238,000
    z6	-14,000	-42,000	-77,000
    (Константа)	-16,849	-144,015	-478,849

     

     

    Таблиця 7.

                                                         Результаты классификации

       

     

      

      

     

      

      

    		KlasDiscr	Предсказанная принадлежность к группе			Итого
    			1,00	2,00	3,00
    Исходные
    	Частота	1,00	2	0	0	2
    		2,00	0	6	0	6
    		3,00	0	0	2	2
    	%	1,00	100,0	,0	,0	100,0
    		2,00	,0	100,0	,0	100,0
    3,00		,0	,0	100,0	100,0

    

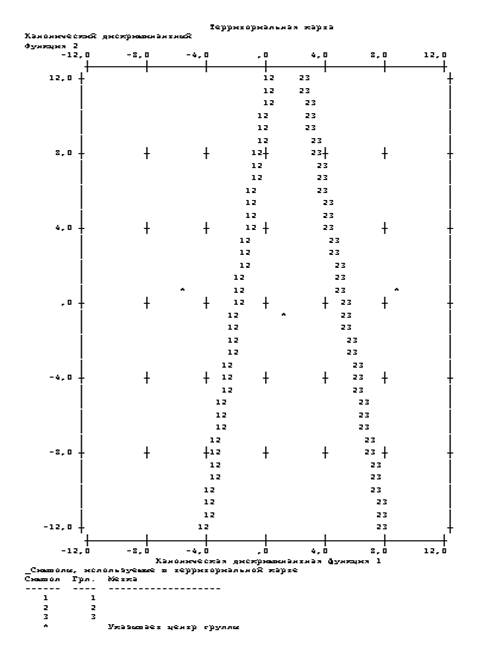
    Рис. 10. Територіальна карта результатів ПСП SPSS дискримінантного аналізу за даними табл.1

     

    Для оцінки надійності теста коефіцієнта  Кьюдера-Річардсона проводяться обчислення за наступною формулою:

    

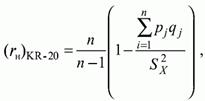
    де рj - частка правильних відповідей на j-е завдання; qj - частка неправильних відповідей, qj = 1 - рj; S²_x-дисперсія з розподілу спостережуваних балів; n - число завдань тесту.

    З використанням даних табл. 1 коефіцієнт  Кьюдера-Річардсона обчислюється наступним чином. Для вихідної матриці даних підрахована раніше дисперсія S²_x = 6,89, а частки правильних відповідей виходять розподілом чисел Rj в останньому рядку матриці на 10. Тоді сума творів часткою правильних і неправильних відповідей буде 0,9 • 0,1 + 0,8 • 0,2 + 0,7 • 0,3 + 0,6 • 0,4 + 0,5 • 0,5+ 0,5 • 0,5 + 0,3 • 0,7 + 0,4 • 0, 6 + 0,2 • 0,8 + 0,1 • 0,9 = 1,9 і коефіцієнт надійності

    

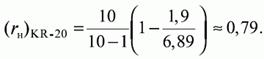
    Як правило, тести з надійністю менше 0,8 вважаються непридатними в професійно організованих службах і центрах тестування. Значення коефіцієнта надійності, що перевищують 0,9, свідчать  про високу якість тесту. Вони вкрай бажані, але не часто трапляються. Зазвичай в тестологічній  практиці надійність тестів коливається в інтервалі (0,8; 0,9). Обчислений коефіцієнт  Кьюдера-Річардсона (r_н)_KR-20=0,8 свідчить про високу надійність цього тесту.

    Конструювання оптимальних тестів  на основі параметричної оцінки тестових завдань базується на застосуванні однопараметричної моделі Раша та двопараметричної моделі Бірнбаума [8]

    Успіх учасника тестування при розв’язанні деякого тестового завдання залежить від двох факторів:складності завдання і рівня підготовки учасника. Ймовірність того, що деякий учасник вірно виконає конкретне завдання, є функцією щонайменше двох аргументів: рівня підготовки учасника тестування S та рівня складності даного завдання t: P =P(S,t) .Таку функцію називають функцією успіху. Якщо вигляд функції успіху відомий, то за результатами випробувань методами математичної статистики з певною точністю можна оцінити аргументи цієї функції, в тому числі і рівень складності завдань:

    

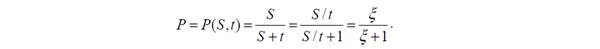
    Ця найпростіша модель вперше дала можливість об’єктивно визначати співвідношення між учасниками тестування і тестовими завданнями довільних рівнів підготовки та складності.

    Якщо ввести позначення

    

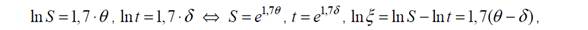
    то функція успіху матиме вигляд

    

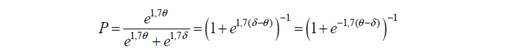
    і буде називатися основною логістичною моделлю Раша.

    Ймовірність успіху залежить лише від різниці q -d , і тому модель Раша є однопараметричною.

    Двопараметрична модель А. Бірнбаума має наступний вигляд:

    

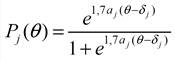
    де a_j – другий параметр, що характеризує диференційовану здатність завдання при зміні різних значень q та ймовірність угадування правильної відповіді на j -е завдання. Оскільки значення   a_j =1 відповідає однопараметричній моделі Раша, тому в даній роботі  ми обмежемось цією моделлю

    Розглянемо модель Раша більш детально. Нехай тест складається із m різних завдань,тест виконують n студентів. Позначимо через x_ij числову оцінку успішності виконання j –ого завдання і -им студентом. Якщо і -ий студент вірно виконав j -те завдання, то x_ij =1 . Якщо невірно, то x_ij =0 . Результати тестування представляються у вигляді матриці результатів { x_ij }, де i =1,n , j =1,m.

    Обчисливши p_i=(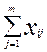)/m  (частка правильних відповідей і -ого студента на всі завдання тесту та q_i = 1- p_i – частка неправильних відповідей), можна визначити початковий логіт рівня знань кожного студента (тобто початкову оцінку рівня знань і -ого студента у шкалі логітів): .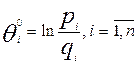

    Обчисливши p_j=(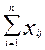)/n   (частка правильних відповідей всіх студентів групи на j –е  завдання та q_j = 1- p_j – частка неправильних відповідей), можна визначити початковий логіт складності завдання (тобто початкову оцінку рівня складності j -ого завдання у шкалі логітів): 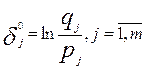_. Отримані значення дозволяють співставити рівень знань студентів із рівнем складності завдань тесту. Якщо q_i -d_j  – від’ємна величина і велика за модулем, то завдання складності d_j є надто важким для студента з рівнем знань q_i  , і воно не буде корисним для виміру рівня знань i -ого студента. Якщо ця різниця додатня і велика за модулем, то завдання надто легке, воно давно освоєно студентом. Якщо q_i =d_j , то ймовірність того, що студент вірно виконає завданя,дорівнює 0,5.

    Після оцінювання значень q і d  у шкалі логітів приступають до обчислення ймовірності Pj(q)  правильного виконання j -ого завдання тесту різними студентами:

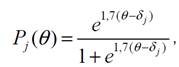    , де θ=( θ₁, θ2,…, θ_n).

    Ймовірність Pj правильного виконання j -ого завдання тесту є зростаючою функцією змінної θ . Очевидно, що чим вищий рівень знань студента, тим більша ймовірність правильного виконання ним j -ого завдання тесту.

    Результати обчислень ймовірностей виконання j-ого завдання і-м студент том за даними табл.1 з використанням моделі Раша та двопараметричної  моделі А. Бірнбаума, за умови a_j =1 приведені в табл. 8.

    Таблиця 8.

    Таблиця ймовірності P_j(θ_i) правильного виконання j -ого завдання

    тесту i-м студентом

    

    

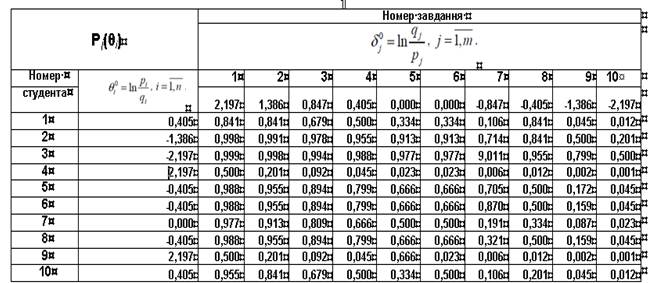
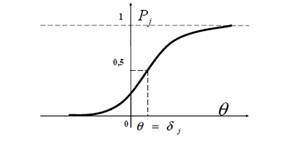
    Рис.11. Характеристична крива j -ого завдання

    Характеристична крива j –ого завдання тесту показує взаємозв’язок між значеннями незалежної змінної q і значеннями  P_j. Точці перегину характеристичної кривої відповідає значення  q =d_j , а P_j  в цій точці дорівнює 0,5. Таким чином, студент із рівнем знань, що дорівнює складності j -ого завдання тесту, відповість на нього правильно з ймовірністю 0,5. Для студентів з рівнем знань набагато більшим, ніж d_j , ймовірність правильної відповіді на це завдання прямує до одиниці. Якщо ж значення q розміщені достатньо далеко від значення  q =d_j і зліва від точки перегину, то ймовірність правильного виконання j -ого завдання буде прямувати до нуля.

    Висновки.

    1.    Принцип роботи автоматизованої системи тестування  повинен ґрунтуватися на критеріях математико-статистичних методів аналізу, які дають  можливість перевіряти тестові завдання на наявність прихованих дефектів, які неможливо виявити із застосуванням експертних методів.

    2.    За допомогою значень точкового бісеріального коефіцієнта кореляції можна оцінити валідність окремих завдань тесту. Точковий  бісеріальний  коефіцієнт кореляції підраховує кореляцію між результатами виконання кожного завдання (дихотомічна шкала) і сумою балів випробовуваних (інтервальна шкала) за завданнями тесту. Вказує, наскільки добре дане ТЗ розрізняє екзаменованих з високим балом і екзаменованих з низьким балом. Може змінюватися від  - 1 до + 1.  Якщо ця величина дорівнює 0, то це означає, що усі екзаменовані відповіли однаково добре або однаково погано.

    3.    Для дослідження надійності тесту   використовується  двофакторний дисперсійний аналіз без повторних вимірювань, де в якості факторів використовуються тестовані та завдання, а в якості залежної змінної виступають первинні бали. З використанням результатів двофакторного дисперсійного аналізу без повторних вимірювань обчислюється коефіцієнт генералізаціі. Коефіцієнт генералізаціі дозволяє зі статистичних позицій оцінити надійність тестових вимірювань. Значення коефіцієнта надійності, що перевищують 0,9, говорять про високу якість тесту. Зазвичай в тестологічнихх практиці надійність тестів коливається в інтервалі (0,8; 0,9).

    4.    Метод кластерного аналізу матриці результатів { x_ij }, де i =1,…,n ,  j = 1,…, m використовуться для кластеризації n тестованих на три  кластери за якістю знань: слабкий, середній, високий рівень. Якщо кількість тестованих в кластерах для слабкого і висого рівня знань не перевищує 17%, то тест вважається якісним.

    5.    Визначення і розрахунок показників якості тестових завдань, відбракування завдань проводиться з використанням методу дискримінантного аналізу за кластерами тестованих побудованими методом кластерного аналізу. Результати класифікації таблиці дискримінантного аналізу свідчать наскільки відсотків відрізняється прогнозована приналежність тестованих до кластера співпадає або відрізняється від відсотка кластера навчальної вибірки. Якщо відсоток некоректної класифікації знаходиться в межах 16%, то тест вважається якісним. Тестові завдання, які всі тестовані виконали відбраковуються як легкі з ймовірністю 1, аналогічно якщо всі тестовані не виконали завдання  то відбраковуються як занадто важкі.

    6.    Успіх учасника тестування при розв’язанні деякого тестового завдання залежить від двох факторів: складності завдання і рівня підготовки учасника. Ймовірність того, що деякий учасник вірно виконає конкретне завдання j, є функцією щонайменше двох аргументів: рівня підготовки учасника тестування S та рівня складності даного завдання θj : P =P(S, θj) . Конструювання оптимальних тестів  на основі параметричної оцінки тестових завдань базується на застосуванні однопараметричної моделі Раша та двопараметричної моделі Бірнбаума для обчислення матриці значень ймовірності того, що деякий учасник вірно виконає конкретне завдання. Очевидно, що чим вищий рівень знань студента, тим більша ймовірність правильного виконання ним j -ого завдання тесту.

    Враховуючи принцип індивідуалізації навчання, для більш грунтовного вирішення необхідний додатковий аналіз учасників тестування з використанням моделі Раша та двопараметричної  моделі А. Бірнбаума та побудови  характеристичних кривих тестових завдань.
    

    
    

    Список використаних джерел

    1.        Кухаренко В.М. Розвиток дистанційного навчання на сучасному етапі. – Науковий вісник Національної академії статистики, обліку та аудиту. Зб. наук. праць – №2, 2012. – с. 117-121.

    2.        Красін М.А., Карпов В.І., Товмаченко Н.М. Перспективний підхід до організаціі навчального процесу. Досвід розвитку вищої освіти у Польщі //Науковий вісник Національної академії статистики , обліку та аудиту.-2013.-№ 4.-С. 109-118.

    3.        Биков В.Ю., Кухаренко В.М. та ін. Технологія створення дистанційного курсу: Навчальний посібник /за ред. В.Ю. Бикова та  В.М.  Кухаренка - К.: Міленіум, 2008. - 324 с.

    4.        L.V.Deryhlazov,V.M.Kukharenko,L.P.Perkhun,N.M.Tovmachenko The Models of Distance Forms of Learning in  National Academy of Statistics, Accounting and Audit //Науковий вісник Національної академії статистики , обліку та аудиту.-2017.-№ 3.-С. 79-89

    5.        Дериглазов Л.В., Кухаренко В.М., Перхун Л.П., Товмаченко Н.М. Досвід впровадження і використання СДН “Прометей” і Moodle в Національній академії статистики, обліку та аудиту. П’ята міжнародна науково-практична конференція «MoodleMoot Ukraine 2017. Теорія і практика використання системи управління  навчанням Moodle». (Київ, КНУБА, 26-27 травня 2017 р.): тези доповідей. – К.: КНУБА, 2017. – С. 13

    6.        Мокрієв М.В. Аналіз тестових завдань засобами Moodle // П’ята міжнародна науково-практична конференція «MoodleMoot Ukraine 2017. Теорія і практика використання системи управ ління навчанням Moodle». (Київ, КНУБА, 26-27 травня 2017 р.): тези доповідей. – К.: КНУБА, 2017. C.18.

    7.        Quiz statistics report // MoodleDocs/ - Режим доступу: https://docs.moodle.org/32/en/Quiz_statistics_report

    8.        Федорук П.І. Адаптивні тести: статистичні методи аналізу результатів тестового контролю знань // Математичні машини і систиеми. - 2007, №3,4. С.122-138.  

    9.        Кухар Л. О. Конструювання тестів. Курс лекцій. : навч. посіб. / Л. О. Кухар, В. П. Сергієнко. —Луцьк, 2010. — 182 с.

    10.     Крокер Л. Введение в классическую и современную теорию тестов /исновки Л. Крокер, Дж. Алгіна. — М. :Логос, 2010. — 668 с.

    11.     Сіницький М.Є. Статистичні інструменти вимірювання якості освіти, ч. 2. Класичний підхід. – Науковий вісник НАСОА, №1. – Київ: НАСОА, 2015. – с. 75-86.

    1.        Кухаренко В.М. Розвиток дистанційного навчання на сучасному етапі. – Науковий вісник Національної академії статистики, обліку та аудиту. Зб. наук. праць – №2, 2012. – с. 117-121.

    2.        Красін М.А., Карпов В.І., Товмаченко Н.М. Перспективний підхід до організаціі навчального процесу. Досвід розвитку вищої освіти у Польщі //Науковий вісник Національної академії статистики , обліку та аудиту.-2013.-№ 4.-С. 109-118.

    3.        Биков В.Ю., Кухаренко В.М. та ін. Технологія створення дистанційного курсу: Навчальний посібник /за ред. В.Ю. Бикова та  В.М.  Кухаренка - К.: Міленіум, 2008. - 324 с.

    4.        L.V.Deryhlazov,V.M.Kukharenko,L.P.Perkhun,N.M.Tovmachenko The Models of Distance Forms of Learning in  National Academy of Statistics, Accounting and Audit //Науковий вісник Національної академії статистики , обліку та аудиту.-2017.-№ 3.-С. 79-89

    5.        Дериглазов Л.В., Кухаренко В.М., Перхун Л.П., Товмаченко Н.М. Досвід впровадження і використання СДН “Прометей” і Moodle в Національній академії статистики, обліку та аудиту. П’ята міжнародна науково-практична конференція «MoodleMoot Ukraine 2017. Теорія і практика використання системи управління  навчанням Moodle». (Київ, КНУБА, 26-27 травня 2017 р.): тези доповідей. – К.: КНУБА, 2017. – С. 13

    6.        Мокрієв М.В. Аналіз тестових завдань засобами Moodle // П’ята міжнародна науково-практична конференція «MoodleMoot Ukraine 2017. Теорія і практика використання системи управ ління навчанням Moodle». (Київ, КНУБА, 26-27 травня 2017 р.): тези доповідей. – К.: КНУБА, 2017. C.18.

    7.        Quiz statistics report // MoodleDocs/ - Режим доступу: https://docs.moodle.org/32/en/Quiz_statistics_report

    8.        Федорук П.І. Адаптивні тести: статистичні методи аналізу результатів тестового контролю знань // Математичні машини і систиеми. - 2007, №3,4. С.122-138.  

    9.        Кухар Л. О. Конструювання тестів. Курс лекцій. : навч. посіб. / Л. О. Кухар, В. П. Сергієнко. —Луцьк, 2010. — 182 с.

    10.     Крокер Л. Введение в классическую и современную теорию тестов /исновки Л. Крокер, Дж. Алгіна. — М. :Логос, 2010. — 668 с.

    11.     Сіницький М.Є. Статистичні інструменти вимірювання якості освіти, ч. 2. Класичний підхід. – Науковий вісник НАСОА, №1. – Київ: НАСОА, 2015. – с. 75-86.

  • Форум обговорення доповіді